Determinantes

Olá, seguindo o que foi dito na postagem anterior, estou seguindo com o conteúdo do Terceiro Bimestre.

Agora dando atenção aos fofinhos do Segundo Ano esta postagem esta relacionada aos Determinantes.

Seguindo a ordem anterior, primeiro a teoria e depois a prática.

Espero que vocês aproveitem bastante.


Determinantes:
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn).

A toda matriz quadrada está associado um número ao qual damos o nome de determinante.



Determinante de 2ª ordem:

Dada a matriz , de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por: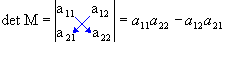

Determinante de 3ª ordem:

Regra de Sarrus:

O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus. Acompanhe como aplicamos essa regra para .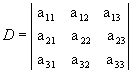

1º passo: Repetimos as duas primeiras colunas ao lado da terceira:

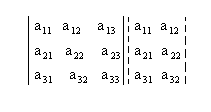
2º passo: Encontramos a soma do produto dos elementos da diagonal principal e subtraímos com a soma do produto dos elementos da diagonal secundária.

Assim:

Para praticar:

Agora que você já viu uma parte da teoria de determinantes, vamos por em prática resolvendo alguns exercícios.

• Cálculo do Determinante de uma matriz 3x3

Aproveitem bastante.

Um abraço a todos

Fonte de Consulta: Só Matemática

Funções (segunda parte)

Olá Florzinhas e Amorzinhos. Depois de bastante tempo estou postando novamente.

Essas próximas postagens serão relativas aos conteúdos do Terceiro Bimestre, e desta vez serão usados massivamente.

Para o Primeiro Ano, teremos a continuação do conteúdo de Funções, justamente do que trataremos agora, que são as Funções Afins, ou Funções Polinomiais do Primeiro Grau.

Primeiro, iniciaremos com a definição seguida de jogos ou exercícios como sempre faço. Espero que vocês aproveitem.

Definição:

Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a é diferente de zero.

Na função f(x) = ax + b, o número a é chamado coeficiente angular da reta e o número b é chamado coeficiente linear da reta.

Veja alguns exemplos de funções polinomiais do 1º grau:

f(x) = 5x - 3, onde a = 5 e b = - 3

f(x) = -2x - 7, onde a = -2 e b = - 7

f(x) = 11x, onde a = 11 e b = 0

Zero da Função:

Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, o número real x tal que f(x) = 0.

Crescimento e decrescimento da Função:

• A função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo

• A função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo

Gráfico da Função:

O gráfico de uma função polinomial do 1º grau, y = ax + b, é uma reta oblíqua aos eixos x e y.

Para Praticar:

Agora que você já conhece alguma coisa das Funções do Primeiro Grau, aproveite pra testar os seus conhecimentos acessando aos links a seguir:

• O Comportamento dos Gráficos
• Contruindo Gráficos a partir da Fórmula

Um beijão a todos.

Fonte da Teoria: Só Matemática